| 1. | Odredite tačnost navedenih tvrdnji. Neke od njih se odnose na ranije upotrebljen primer histograma na kojima su prikazani rezultati studenata pet fakulteta koji su polagali isti test sposobnosti na kome su mogli da osvoje od 0 do 100 poena.

|
||
| T | N | ||
| Vrednost t-testa bi ukazala da nema statistički značajne razlike u uspehu studenata fakulteta A i C | |||
Distribucije A i C su gotovo potpuno simetrične i imaju jednake raspone. To znači da su vrednosti njihovih aritmetičkih sredina veoma slične i iznose približno 50 poena. Razlika ovih aritmetičkih sredina je nedovoljno velika, posebno uzimajući u obzir varijabilnost rezultata u obe grupe. Stoga t-test sigurno ne bi bio statistički značajan.
| |||
| Razlika dve aritmetičke sredine mora da bude veća od 1,96 da bi bila statistički značajna | |||
Granična vrednost od 1,96 odnosi se na t-odnos, tj. odnos razlike aritmetičkih sredina i greške te razlike. Ukoliko je t-vrednost razlike aritmetičkih sredina izračunatih na velikim uzorcima veća od 1,96, možemo je smatrati statistički značajnom na nivou 0,05. Sa druge strane, apsolutna vrednost razlike ne govori ništa o njenoj značajnosti. Razlika od 0,001 (npr. metara) može da bude statistički značajna, a razlika od 100 (npr. kg) ne mora. Značajnost prvenstveno zavisi od varijabilnost pojave unutar grupa i veličina uzorka.
| |||
| Pirsonov koeficijent korelacije dve standardizovane varijable (transformisane u z skorove) uvek je 1 | |||
Standardizacija izmerenih vrednosti varijable ne utiče na njenu korelaciju sa drugim varijablama. Korelacija dve varijable biće potpuno ista i nakon što se vrednosti svake od njih pretvore u z skorove. Štaviše, Pirsonov r može da se izračuna kao prosek sume proizvoda z vrednosti parova rezultata, tako da sam postupak njegovog računanja u stvari podrazumeva prethodnu standardizaciju obe varijable.
| |||
| Vrednost χ2 je uvek nula kada je suma opaženih frekvencija (fo) jednaka sumi teorijskih (ft) | |||
Ova tvrdnja nema smisla jer je jedan od osnovnih uslova za primenu χ2 testa da suma opaženih frekvencija bude jednaka sumi teorijskih. Vrednost χ2 testa biće nula samo ako je u svakoj ćeliji tabele kontingencije fo jednako ft, odnosno onda kada je distribucija opaženih frekvencija potpuno jednaka distribuciji očekivanih.
| |||
| Odnos između koeficijenata korelacije i odgovarajućih koeficijenata determinacije je nelinearan | |||
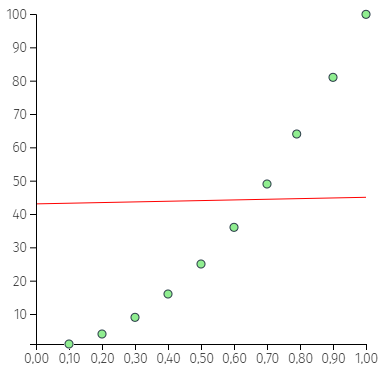 Koeficijent determinacije ukazuje na procenat zajedničkog variranja dve varijable, odnosno procenat varijanse jedne varijable koji se može objasniti varijansom druge. Računa se veoma jednostavno, tako što se koeficijent korelacije kvadrira i pomnoži sa 100. Pošto se kvadriranjem, za razliku od sabiranja ili množenja, vrši nelinearna transformacija vrednosti, odnos između koeficijanta korelacije i odgovarjućih koeficijenta determinacije ne može da se predstavi pravom linijom. Na slici levo se vidi da sa porastom koeficijanta koelacije, koeficijent determinacije raste nelinearno. Na primer, varijable koje su u korelaciji od r = 0,10 imaju 1% zajedničke varijanse, za r = 0,40 taj procenat je 16%, a za 0,70 je 49%.
Koeficijent determinacije ukazuje na procenat zajedničkog variranja dve varijable, odnosno procenat varijanse jedne varijable koji se može objasniti varijansom druge. Računa se veoma jednostavno, tako što se koeficijent korelacije kvadrira i pomnoži sa 100. Pošto se kvadriranjem, za razliku od sabiranja ili množenja, vrši nelinearna transformacija vrednosti, odnos između koeficijanta korelacije i odgovarjućih koeficijenta determinacije ne može da se predstavi pravom linijom. Na slici levo se vidi da sa porastom koeficijanta koelacije, koeficijent determinacije raste nelinearno. Na primer, varijable koje su u korelaciji od r = 0,10 imaju 1% zajedničke varijanse, za r = 0,40 taj procenat je 16%, a za 0,70 je 49%.
| |||
| Ako dve varijable imaju jednake M i jednake s korelacija među njima je sigurno statistički značajna | |||
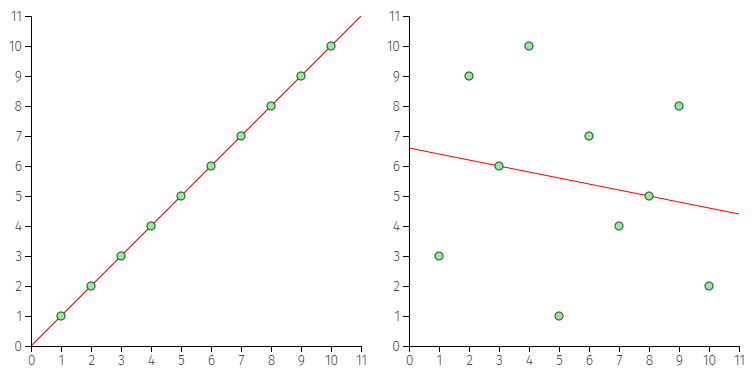 Iako se koriste prilikom računanja Pirosonovog koeficijenta korelacije, vrednosti aritmetičkih sredina i standarnih devijacija varijabli ne govore ništa o njihovoj povezanosti. Pogledajte primere na slici levo. U oba slučaja, izmerene vrednosti svih varijabli su iste – od 1 do 10 npr. poena. To znači da su M i s za sve prikazane varijable potpuno iste. Međutim, u prvom slučaju vrednosti po parovima su potpuno iste (npr. 1–1, 2–2) tako da je korelacija maksimalna. U drugom slučaju, uparene su različite vrednosti (npr. 1–3, 10–2) tako da je korelacija niska.
Iako se koriste prilikom računanja Pirosonovog koeficijenta korelacije, vrednosti aritmetičkih sredina i standarnih devijacija varijabli ne govore ništa o njihovoj povezanosti. Pogledajte primere na slici levo. U oba slučaja, izmerene vrednosti svih varijabli su iste – od 1 do 10 npr. poena. To znači da su M i s za sve prikazane varijable potpuno iste. Međutim, u prvom slučaju vrednosti po parovima su potpuno iste (npr. 1–1, 2–2) tako da je korelacija maksimalna. U drugom slučaju, uparene su različite vrednosti (npr. 1–3, 10–2) tako da je korelacija niska.
| |||
| Povezanost rezultata studenata fakulteta D i studenata fakulteta E može da se izrazi koeficijentom r | |||
U ovom primeru ne treba gledati da li su ispunjeni uslovi koji se tiču normalnosti raspodele ili nivoa merenja varijabli, već da li je korelaciju uopšte moguće izračunati. Da bi se izračunao bilo koji koeficijent korelacije neophodno je postojanje uparenih rezultata. U ovom primeru ne postoji apsolutno nikakav osnov da se rezultat nekog studenta sa fakulteta D upari sa rezultatima nekog od studenata fakulteta E. Čak i kada bi se takva veza na neki način ostvarila, nejasno je kakav bi zaključak mogao da se donese pošto su očigledno u pitnju "veštački" upareni ispitanici, a ne prirodno kao u odnosu roditelj–dete. U ovom drugom slučaju, zaista bi moglo da se konstatuje da je npr. viši agresivnosi roditelja povezan za nivoom agresivnosti njihove dece.
| |||
| Kada bi se studenti podelili na bolje i lošije od 50 poena, χ2 između grupa B i C bio bi značajan | |||
Ako studente oba fakulteta podelimo na one koji su osvojili manje od 50 poena i one koji su osvojili 50 ili više poena, u grupu studenata fakulteta B bi bilo proporcionalno više lošijih rezultata. Za razliku od toga, u grupi studenata fakulteta C broj loših i dobrih bi bio približno isti. Zbog ove velike razlike u porporcijama dobrih i loših studenata vrednost χ2 testa bi bila statistički značajna.
| |||
| C koeficijent će biti jednak nuli ako se u svim ćelijama tabele kontingencije nalaze iste vrednosti | |||
Ukoliko se u svim ćelijama tabele kontingencije nalaze iste vrednosti teorijske frekvencije će biti potpuno iste kao i očekivane za svaku od tih ćelija. Sami tim, vrednost χ2 će biti nula, pa će tako i C koeficijent biti jednak nuli. Drugim rečima, promene na jednoj varijabli nemaju nikakve veze sa promenama na drugoj.
| |||
| Vrednost t-testa za zavisne uzorke ne može da bude manja od -1 niti veća od 1 | |||
Vrednosti t-testa nisu ograničene ni sa gornje ni sa donje strane, bez obzira na vrstu (zavisni ili nezavisni). Što je razlika aritmetičkih sredina veća, a greška te razlike manja, t vrednost će biti veća.
| |||
| 2. | Ispitivana je brzina prolaska kroz složeni lavirint na uzorku predškolske dece. I pre i posle uvežbanja u proseku im je trebalo minut i 25 sekundi za savladavanje lavirinta. Kolika treba da bude vrednost standardne greške razlike aritmetičkih sredina da bi t-test bio značajan na nivou 0,01? | ||
|
|
|||
Za rešavanje ovog zadataka nije potrebno nikakavo poznavanje gormula, pa čak ni statističke logike računanja t-testa. Činjenica da ne postoji nikakva razlika između prvog i drugog merenja trebalo bi da bude dovoljna informacija za zaključak da ne postoji način da se nula proglasi statistički značajnom, odnosno da ne postoji vrednost standardne greške razlike koja bi rezultirala apsolutnom vrednošću t-testa od nule.
| |||
| 3. | 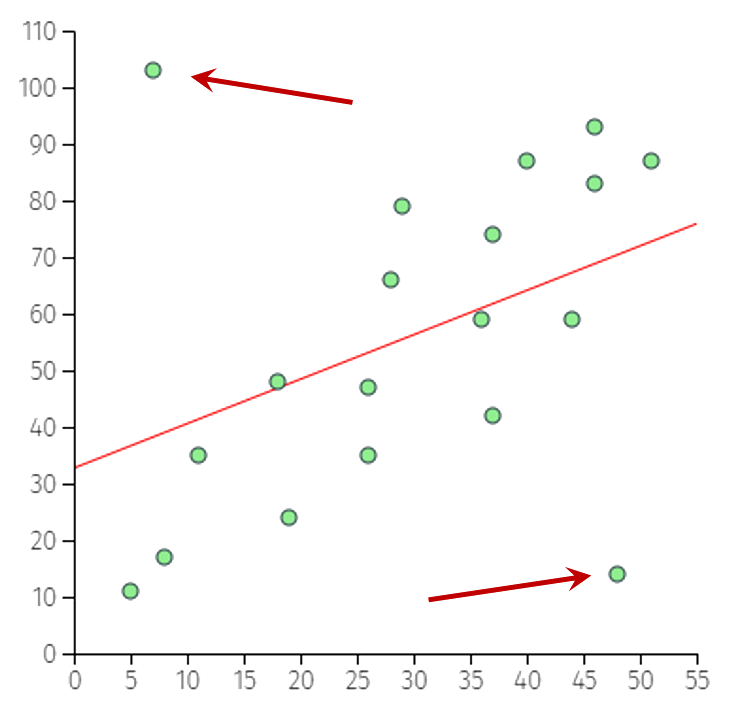 Pirsonov koeficijent korelacije varijabli prikazanih na dijagramu sa leve strane iznosi r = 0,41. Koliki bi bio koeficijent korelacije kada bi se uklonila dva aberantna rezultata označena strelicama? Pirsonov koeficijent korelacije varijabli prikazanih na dijagramu sa leve strane iznosi r = 0,41. Koliki bi bio koeficijent korelacije kada bi se uklonila dva aberantna rezultata označena strelicama?
|
||
Nakon uklanjanja aberantnih rezultata koeficijent korelacije će ostati pozitivan i značajno će se povećati, jer raspršenje oko regresione prave postaje relativno malo. Velika razlika između stepena sadašnjeg raspršenja i onoga nakon uklanjanja autlajera sugeriše da bi povećanje koeficijenta bilo znatno veće od 0,1 (0,51-0,41).
| |||
| 4. | U tabeli kontingencije prikazani su odgovori studenata i studentkinja na pitanje u kojoj meri su zadovoljni uslugama studentskog veb servisa (1 – potpuno nezadovoljan/na, 2 – uglavnom zadovoljan/na i 3 – veoma zadovoljan/na). Odgovorite na postavljena pitanja.
|
||||||||||||||||||||||
| a) Koliki bi bio nivo verovatnoće (p) χ2 testa kada bi se njime testirala statistička značajnost razlike u stavu prema uslugama veb servisa između studenata i studentkinja | |||||||||||||||||||||||
|
|
|||||||||||||||||||||||
Na osnovu podataka u tabeli kontingencije da je proporcionalni odnos različitih odgovora (1 – 3) potpuno isti u grupi studenata i studentkinja. Na primer, 15 od 30 studenata koji su dali odgovor 1 je proporcionalno isti kao 45 od 90 studentkinja (0,5 ili 50%). Samim tim, vrednost χ2 bi bila 0, jer ne postoji nikakva razlika među grupama. Ukoliko je vrednost statističkog test nulta, prateći nivo verovatnoće je 1. U ovom slučaju to znači da je stopostotna verovatnoća da se dobije χ2 vrednost veća ili jednaka nuli.
| |||||||||||||||||||||||
| b) Kolika bi bila vrednost t-testa kada bi se njime testirala statistička značajnost razlike u stavu prema uslugama veb servisa između studenata i studentkinja? | |||||||||||||||||||||||
|
|
|||||||||||||||||||||||
U ovom istraživanju se razlikuje samo broj studenata od broja studentkinja. Slično prethodnom odgovoru, može se zaključiti da su njihovi stavovi potpuno isti, odnosno da je prosek vrednosti odgovora za studente ((15 + 10 + 5) : 30) identičan proseku odgovora studentkinja ((45 + 30 + 15) : 90). To znači da je razlika između aritmetičkih sredina, a samim tim i vrednost t-testa, jednaka nuli.
| |||||||||||||||||||||||
| c) Koliki bi bio broj stepeni slobode kada bi se za analizu primenio χ2 test, a koliki kada bi se primenio t-test? | |||||||||||||||||||||||
|
|
|||||||||||||||||||||||
Broj stepeni slobode χ2 testa računa se po formuli (k - 1) · (r - 1) gde su k i r broj kolona i redova u matrici kontingencije, neračunajući marginalne ćelije. Broj stepeni t-testa za nezavisne uzorke računa se po formuli N - 2 gde je N ukupan broj merenja, odnosno ispitanika.
| |||||||||||||||||||||||
| 5. | Na podacima prikupljenim u grupi od 200 ispitanika obavljena je regresiona analiza koja je rezultirala regresionom jednačinom y' = 24,3 - 4,5 · x. Koja od navedenih tvrdnji je sigurno tačna? | ||
|
|
|||
Na osnovu jednostavne regresione jednačine nije moguće doneti bilo kakav zakljčak o visini ili značajnosti pratećeg koeficijenta korelacije, izuzev ako je ona formirana na osnovu standardizovanih vrednosti. To ovde očigledno nije slučaj, jer je a različito od nule, a b izlazi van očekivanog raspona z vrednosti. Koeficijent korelacije, pa tako i regresionu jednačinu, moguće je izračunati na praktično bilo kom skupu podataka, bez obzira na to da li je odnos među varijablama (ne)linearan. To znači da navedena regresiona jednačina može da se odnosi na varijable među kojima je korelacija potpuna, kada je vrednost Σ(y'-y)2 jednaka nuli, ili na varijable koje nisu u značajnoj korelaciji. Jedini pouzdan zaključak koji je moguće doneti na osnovu date jednačine jeste da je korelacija među varijablama negativna o čemu govori negativan predznak koeficijenta b.
| |||
| 6. | Koji od navedenih statističkih postupaka biste upotrebili za testiranje sledećih hipoteza? | ||
| Ne postoji statistički značajna razlika između broja studenata koji su položili ispit i broja onih koji nisu | |||
U ovom primeru postoji samo jedan uzorak ispitanika koji je podeljen na osnovu kriterijuma da li su položili ispit ili ne. Jedino što istraživač može da uradi χ2 testom za jedan uzorak je da uporedi opažene frekvencije (npr. 60 – 40) sa očekivanim na osnovu pretpostavke da nema razlike u prolaznosti (50 – 50). Pri tome mora da bude ispunjen uslov da suma opaženih frekvencija bude jednaka sumi teorijskih.
| |||
| Ne postoji uticaj nadmorske visine na brzinu trčanja grupe trkača koji su najpre trčali na stazi pored mora, a potom na planinskoj stazi | |||
Brzina trčanja je varijabla razmernog nivoa što omogućava primenu t-testa. Pošto je u pitanju ista grupa trkača koji su najpre trčali na nižoj, a potom na višoj stazi, potrebno je primeniti nacrt za zavisne uzorke.
| |||
| Ne postoji značajna razlika u stavu studenata prema kursu iz informatike (pozitivan / negativan) pre i nakon što su položili ispit | |||
Na vrednostima stava kao dihotomne varijable ne bi trebalo računati proseke, pa se tako mogu uporediti samo proporcije, tj. frekvencije različitih odgovora pre i posle polaganja ispita (χ2). Pošto su u pitanju ponovljena merenja, trebalo bi primeniti tehniku koja je namenjena zavisnim uzrocima, npr. Maknimarov test.
| |||
| Ne postoje međupolne (muško / žensko) razlike kod učenika osmog razreda u izboru srednje škole (stručna / gimnazija / umetnička) | |||
Dve nezavisne grupe se porede na varijabli nominalnog nivoa, tako da je jedini opravdani izbor χ2 test.
| |||
| Ne postoji povezanost između pola učenika osmog razreda (muško / žensko) i izbora srednje škole (stručna / gimnazija / umetnička) | |||
U prethodnom pitanju tražena je razlika među grupama. Ukoliko ta razlika postoji, onda je izvesno da postoji i povezanost između pola i izbora škole. Međutim, vrednost χ2 testa nije standardna mera povezanosti varijabli. Stoga ga treba transformisati u koeficijent kontingencije C uzimajući u obzir veličinu uzorka.
| |||
| Ne postoji razlika u broju bodova osvojenih na testu znanja između studenata koji su pohađali vežbe ponedeljkom i onih koji su ih pohađali petkom | |||
Dve grupe studenata porede se na varijabli koja je najmanje intervalnog nivoa. Opravdano je primeniti t-test za nezavisne uzorke.
| |||
| Ne postoji značajna povezanost između zadovoljstva poslom izmerenog upitnikom i broja povreda na radu u određenom vremenskom periodu | |||
Pomenute varijable su intervalnog, odnosno razmernog nivoa, tako da se njihova povezanost može izraziti Pirsonovim koeficijentom korelacije. To naravno nije jedini uslov i uvek je potrebno proveriti i izgled distribuije. Na primer, očekuje se da broj povreda na radu nije normalno distribuiran, odnosno da je distribucija ovih vrednosti pozitivno iskošena, jer će većina zaposlenih ipak imati jednu ili nijednu povredu. Stoga bi u ovom primeru verovatno bilo prikladnije primeniti Spirmanov ρ.
| |||