| 1. | Odredite nivo merenja navedenih varijabli. Opcije odgovora su No(minalni), Or(dinalni), In(tervalni), R(acio) D(iskrenta) i R(acio) K(ontinuirana). |
|||||
| No | Or | In | RD | RK | ||
| Zadovoljstvo uslugom restorana na skali od 1 do 5 | ||||||
Odgovori na tzv. Likertovim skalama načelno se tretiraju kao ordinalna merenja. Iako su "razmaci" između ocena naizgled jednaki (npr. 1–2 i 2–3), ti intervali su potpuno subjekitvni i baziraju se na procenama ispitanika. Drugačije rečeno, istraživač može da zaključi samo da je ispitanik koji je zaokružio odgovor 2 verovatno zadovoljniji od onoga koji je zaokružio odgovor 1, ali nije moguće odgovoriti na pitanje za koliko je on tačno zadovoljniji. Stoga se i školske ocene smatraju ordinalnim vrednostima, jer petica iz jedne škole ne mora nužno da znači da đak ima više znanja od nekoga ko je u drugoj školi dobio 4. Za razliku od toga, đak koji je visok 170 cm sigurno je viši od onoga koji je visok 168 cm, a ide u drugu školu. Stoga visinu smatramo varijablom višeg nivoa merenja.
| ||||||
| Broj neopravdanih časova koje je učenik dobio u toku polugodišta | ||||||
Vrednosti nastale prebrojavanjem načelno se mogu smatrati diskretnim varijablama razmernog nivoa. Međutim, njihova upotrebljivost u statističkim analizama zavisi od broja, tj. raspona mogućih vrednosti. Na primer, broj automobila u domaćinstvu će za većinu ispitanika imati vrednosti 0 ili 1 što znači da će takva varijabla u najboljem slučaju moći da se upotrebi kao kategorijalna, odnosno kao kriterijum na osnovu koga će se domaćinstva podeliti u dve grupe. Sa druge strane, broj bodova osvojenih na testu, npr. u rasponu od 0 do 100, takođe je diskretna varijabla razmernog nivoa, ali omogućava mnogo više operacija koje istraživač može da obavi nad njenim vrednostima.
| ||||||
| Posedovanje vozačke dozvole | ||||||
Slično obrazloženju datom u prethodnom pitanju, odgovor "Da" ili "Ne" u ovom slučaju, iako govori o tome da neko ima više vozačkih dozvola od nekog drugog, opravdano je tretirati samo kao varijablu nominalnog nivoa.
| ||||||
| Brzina reakcije za vizuelni stimulus | ||||||
Iako ne postoji osoba koja bi mogla da odreaguje na izloženi vizuelni stimulus za 0 sekundi, niti instrument koji bi mogao da izmeri brzinu na desetoj decimali, ova varijabla je po prirodi razmerna i kontinuirana. Apslutna nula postoji kao podeok na skali kojom se meri protok vremena od izlaganja stimulusa do reakcije, a broj podeoka je neograničen.
| ||||||
| Zanimanje ispitanika | ||||||
Zanimanja (npr. pekar, stolar, programer, profesor) označavaju samo pripadnost klasi i ne govore ni o kakvom kvantitativnom svojstvu ispitanika. U pitanju je kvalitativna, odnosno nominalna varijbla.
| ||||||
| Stručna sprema ispitanika | ||||||
Za razliku od zanimanja, stručna sprema omogućava poređenje ispitanika po količini nekog svojstva, u ovom slučaju obrazovanja. Iako bi se obrazovanje moglo izraziti vremenom provedenim u školovanju, to nije praksa. Uobičajeno je da se obrazovanje izražava stepenima stručne spreme između kojih intervali nisu jednaki, ali omogućavaju definisanje relacije manje–više, kao npr. osnovna škola, srednja škola, viša škola, fakultet, doktorat.
| ||||||
| Jedinstveni matični broj građana | ||||||
Iako je u pitanju broj, JMBG nije kvantitavna vrednost kojom se izražava količina nekog svojstva. Čak ni činjenica da se prvih 7 cifara odnosi na datum rođenja osobe ne omogućava nam poređenja, npr. tako što ćemo ispitanike sortirati po starosti. JMBG ima istu (kvalitativnu) funkciju kao i ime ispitanika.
| ||||||
| Redosled upisa studenata izražen brojem indeksa | ||||||
Slično kao i JMBG, broj studentskog indeksa je samo način identifikacije osobe, pa je samim tim opravdano tretirati je kao nominalnu, odnosno kvalitativnu varijablu. Međutim, ukoliko se brojevi dodeljuju redom, ipak je moguće doneti zaključak o tome koji student je upisan ranije, a koji kasnije. To i dalje ne nudi informaciju o tome koliko se neko ranije upisao, pa ipak nije reč o intervalnoj varijabli.
| ||||||
| Prosečni godišnji prihodi domaćinstva | ||||||
U ovom slučaju "ispitanik" čije se svojstvo "meri" je domaćinstvo. Na osnovu prihoda svakog člana domaćinstva računa se prosek koji se potom pripisuje domaćinstvu kao entitetu. Nažalost, vrednost 0 je moguća i zaista označava potpuno odsustvo svojstva "prihodi". S obzirom na to da varijabla može da uzme bilo koju (decimalnu) vrednost od 0 naviše, opravdano je tretirati je kao razmernu i kontinuiranu.
| ||||||
| Dnevna temperatura na skali Celizijusa | ||||||
U pokušajima da se razjasni razlika između intervalnih i razmernih varijabli, u literaturi se obično navodi primer temperature na skali Celzijusa. Ono što ovu varijabli čini intervalnom je nedostatak apsolutne nule. Za objekat koji ima vrednost 0 na ovoj skali ne može se reći da nema temperaturu. Slično je i sa IQ skalama ili rezultatima koji se dobijaju primenom upitnika ličnosti. Na primer, čak i ako osoba ne odgovori pozitivno ni na jedno pitanje koje ukazuje na to da je ona agresivna, njena agresivnost neće biti procenjena kao "nepostojeća". Međutim, ove suptilne razlike između intervalnih i racio varijabli su u suštini nebitne iz aspekta statističke obrade. Štaviše, IQ skalu i skalu agresivnosi bi bilo opravdanije tretirati kao ordinalne, ali je uobičajeno da se zbog dovoljno velikog broja podeoka na njima obavljaju matematičke operacije koju se namenjene varijablama razmernog nivoa.
| ||||||
| 2. | U istraživanju je učestvovalo 20 studenata i studentkinja psihologije, 25 pedagogije i 15 istorije. Svi su popunjavali upitnik koji se sastojao od 10 pitanja vezanih za emotivna stanja u toku pandemije virusa. Na pitanja su odgovarali izražavajući slaganje sa tvrdnjom na skali od 1 do 7. Ukupno 12 studenata nije odgovorilo na 5. pitanje, a njih 9 nije odgovorilo na 8. pitanje u upitniku. Koliko redova i koliko kolona treba da ima matrica sirovih podataka da bi se mogli zabeležiti svi pomenuti prikupljeni podaci o ispitanicima. | ||
| Matrica treba da ima redova i kolona/e. | |||
Ukupan broj ispitanika (studenata) je 60, pa je potrebno da matrica ima toliko redova. Za svakog studenta postoji podatak o polu i studijskog grupi. Pored toga, odgovori na svaku pojedinačnu stavku upitnika tretiraju se kao zasebne varijable. To znači da matrica treba da ima 12 kolona. Činjenica da neki podaci nedostaju ne utiče na dimenzije matrice. To samo znači da će pojedini redovi (studenti) imati prazne kućice u sedmoj (5. pitanje) i desetoj (8. pitanje) koloni.
| |||
| 3. | Za učenike odeljenja IVA i IVB prikazane su zaključne ocene iz matematike uz pomoć dva kružna (torta) dijagrama. Koji zaključak nije mogao da bude donet na osnovu takvog grafičkog prikaza? | ||
|
|
|||
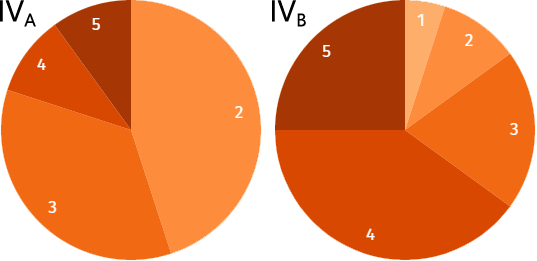 Na osnovu kružnog dijagrama moguće je donositi samo zaključke o udelu (proporciji) određenih vrednosti u ukupnom uzorku merenja. U tom smislu, poređenjem dva kružna dijagrama nije moguće zaključiti kojim od njih je vizualizovan veći broj rezultata. Ukoliko je na jednom dijagramu proporcionalno veći broj ocena 4 i 5 nego na drugom, može se zaključiti da je to odeljenje kao grupa ostvarilo bolji učinak. Međutim, to i dalje ne mora da znači da u prvom odeljenju nema apsolutno više ocena 4 i 5 zato što je u njemu bilo i više đaka.
Na osnovu kružnog dijagrama moguće je donositi samo zaključke o udelu (proporciji) određenih vrednosti u ukupnom uzorku merenja. U tom smislu, poređenjem dva kružna dijagrama nije moguće zaključiti kojim od njih je vizualizovan veći broj rezultata. Ukoliko je na jednom dijagramu proporcionalno veći broj ocena 4 i 5 nego na drugom, može se zaključiti da je to odeljenje kao grupa ostvarilo bolji učinak. Međutim, to i dalje ne mora da znači da u prvom odeljenju nema apsolutno više ocena 4 i 5 zato što je u njemu bilo i više đaka.
| |||
| 4. | Zadatak vam je da na jednom dijagramu prikažete uspeh, tj. broj osvojenih bodova učenika 5 odeljenja na završnom testu iz srpskog jezika. Koji tip grafikona je najprikladniji? | ||
|
|
|||
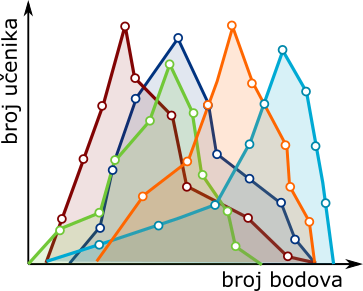 U zadatku je potrebno predstaviti raspodelu bodova po odeljenjima, odnosno prikazati broj đaka koji su osvojili određeni broj bodova, ali za svako odeljenje zasebno. Od punuđenih tipova grafikona, za ove potrebe su pogodni jedino stubičasti dijagram i poligon frekvencija. Pošto se istovremeno prikazuje raspodela bodova za pet odeljenja, veliki broj stubića bi verovatno znatno umanjio preglednost i čitljivost grafikona. Stoga je najprikladnije rešenje poligon, odnosno pet poligona frekvencija, kao što je prikazano na slici. U nastavku udžbenika ćemo pomenuti još neke vrste grafikona koji su pogodni(ji) za prikazivanje raspodela podataka po grupama.
U zadatku je potrebno predstaviti raspodelu bodova po odeljenjima, odnosno prikazati broj đaka koji su osvojili određeni broj bodova, ali za svako odeljenje zasebno. Od punuđenih tipova grafikona, za ove potrebe su pogodni jedino stubičasti dijagram i poligon frekvencija. Pošto se istovremeno prikazuje raspodela bodova za pet odeljenja, veliki broj stubića bi verovatno znatno umanjio preglednost i čitljivost grafikona. Stoga je najprikladnije rešenje poligon, odnosno pet poligona frekvencija, kao što je prikazano na slici. U nastavku udžbenika ćemo pomenuti još neke vrste grafikona koji su pogodni(ji) za prikazivanje raspodela podataka po grupama.
| |||
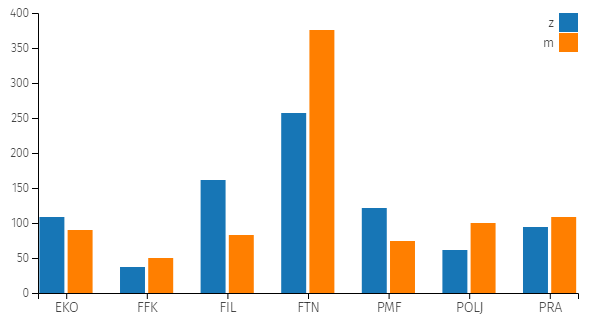
| 5. | Na grafikonu je prikazan broj studenata sedam fakulteta: Ekonomskog (EKO), Fakulteta fizičke kulture (FFK), Filozofskog (FIL), Fakulteta tehničkih nauka (FTN), Prirodno-matematičkog (PMF), Poljoprivrednog (POLJ) i Pravnog (PRA). Odredite koja od navedenih tvrdnji je netačna.
 |
||
|
|
|||
Samo na FTN i FIL ima preko 800 studenata tako da je ukupan uzorak sigurno veći od 1000.
| |||